身近な題材から数学を見つめる

「折り紙」の作図可能性

平面図形や立体など様々な図形や空間の性質について探究する「幾何学」。福井大学では教員を養成する学部に在籍していることもあり、誰でも興味を持てる題材を研究しています。

例えば「折り紙」は数学的に見てとても奥が深い題材です。小中高校の数学で作図を習う際には、定規とコンパスを使っていたかと思います。これは、古代ギリシャで誕生した方法で、三角形や五角形を描くことは可能ですが、七角形や九角形は作図できません。しかし、折り紙を使用するとこれらを作図することが可能であることが１９８０～９０年代に知られるようになりました。折り紙の作図可能性は非常に広いのです。

新たな作図に挑戦

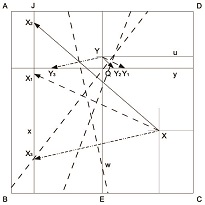正素数多角形の作図に関しては、２０００年代にオーストリアの数学者が正13、17、19角形までを折り紙で作る方法を発表しています。そこで、私は学生とともに、その次に作図可能な多角形を折り紙を用いて作ることに挑戦しました。

正19角形の次に折り紙で作図可能な正素数多角形は正37角形です。まず、複雑な代数方程式を解き、折り紙を折る辺の長さや角度を導き出します。次に35㎝四方の大きな折り紙を４つ折りにしてｘｙ軸の座標に見立て、方程式に従ってどの点・線を、どの順序で折るか設計図を作図していきました。方程式を折り紙に置き換える際にも平方根や立方根を計算する複雑な過程を経る必要があり、非常に苦労しました。このようにして正37角形が実現できたときは１つの山を登ったような達成感がありましたね。

最近では、同じように正73角形の作図を導き出しました。今までに知られていない公式や定理を地道に導きだしていくことは、数学者としての大きな楽しみの一つです。

視野を広く過ごしてほしい

幾何学をはじめとする「数学」に興味を持った大きな理由は、「趣味」によってです。小中学時代から、昆虫の創作折り紙をしたり、マジックやジャグリング、チェスなどに凝っていました。これらを突き詰めて辿り着いたのが「数学」です。学生の皆さんには、いろいろなことに興味を持ち探究してほしいと考えています。興味が広がれば視野が広がり、人間としての幅も広がります。自分が歩む道もきっと見えてくると思いますよ。